理解正则语言的泵引理

26 Apr 2017 , 2600 words

正则语言的泵引理可以用来证明一个语言非正则。

泵引理的原理

泵引理可以用鸽笼原理来理解：把一群鸽子放入几个鸽笼中，如果鸽子数量多于鸽笼数量，那么一定有鸽笼中的鸽子数超过一个。同样，如果把一个字符串输入一个有穷机并被接受，若该字符串长度大于有穷机状态数量，则在运行过程中一定有一些状态被到达了超过一次，换言之出现了循环。

然后根据有穷机的性质，如果出现了循环，那无论循环多少次，还是会回到当前状态来接受接下来的输入，也就是对结果毫无影响。好比坐车，如果从 A 站到 B 站有车，从 B 站到 C 站有车（一个字符串被有穷机接受），那么无论乘客从 B 站下车后随意搭车去什么地方，只要他最终还是回到 B 站（在中间某个或某几个状态循环），他就一定可以再坐车从 B 站到 C 站 （循环不影响结果，构成的新字符串依然会被接受）。

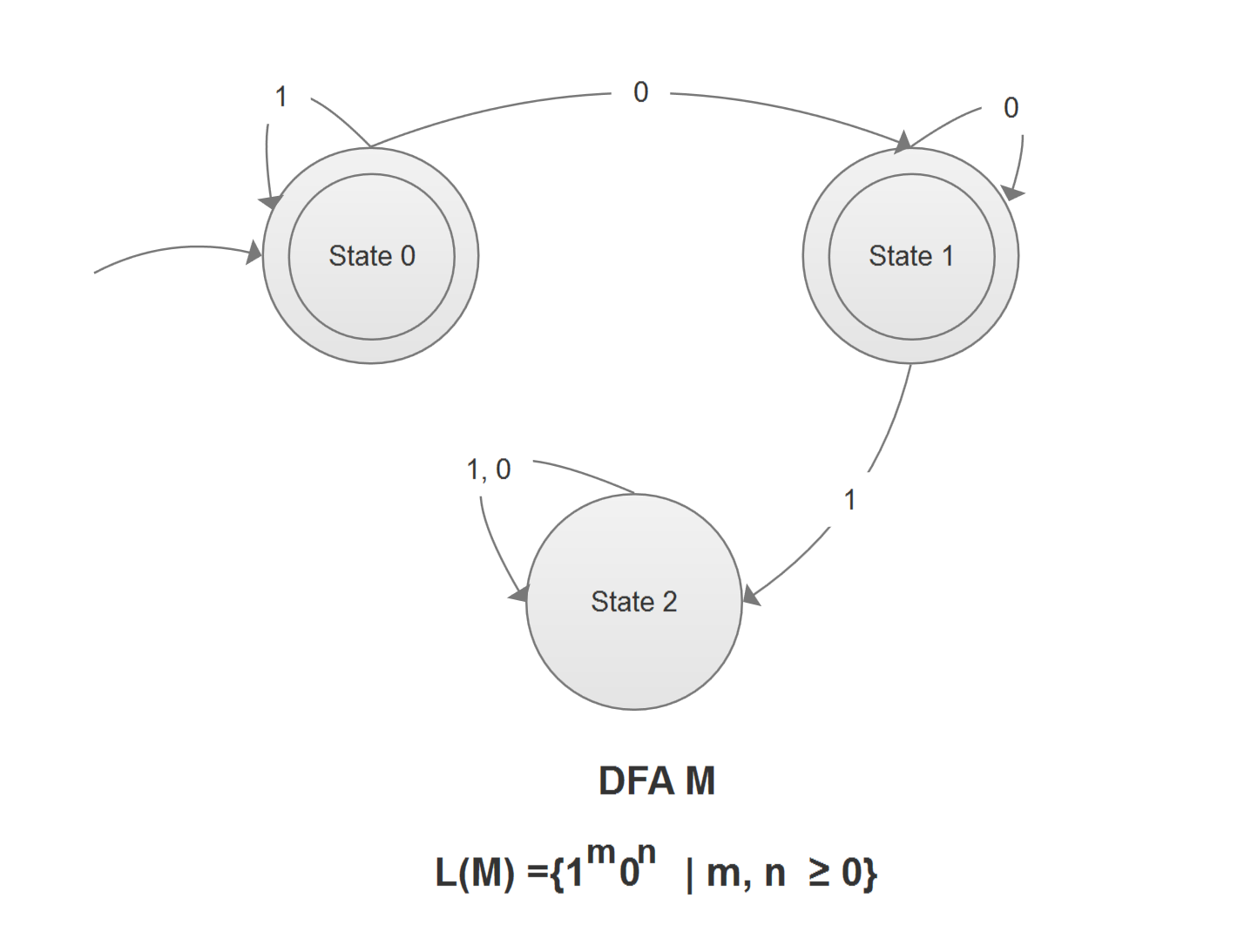
DFA Sample

如例子中接受 L= {0m1n / n, m ≥ 0} 这一语言的有穷机 M 。只要输入的字符串 s (s ∈ L) 长度大于等于 3 就一定会出现循环，而这种循环并不会影响 M 接受 s。

泵引理的正式定义

任何一个正则语言及其对应的有穷机都满足上边的性质，由于中间循环的部分可以随意重复，就好像一个泵能随意抽插，因此被称为泵引理。正式一些的表述如下：

如果一个语言 L 正则，那么存在长度 P，称之为 L 的泵长度。泵长度 P 有这样的性质：任何一个长度大于等于 P 的字符串 s ∈ L，都可以写成 s = xyz 的形式，其中：

  1. xyiz ∈ L (i ≥ 0)
  2. /y/ ＞ 0
  3. /xy/ ≤ P

即，s 可以拆分成 xyz 三部分，y 部分长度大于 0，xy 部分长度加起来小于等于 P，y 不管重复多少次（包括 0 次），所得结果依然属于 L 语言。

回到上边的例子 L= {0m1n / n, m ≥ 0} 中，显然存在长度 P = 3，那么任何一个长度 3 以上属于 L 的字符串 s 都可以被拆分成 xyz 部分并满足那三个条件。如何拆？给定一个 s 的话，往往有很多种拆法，因为只要能让 y 部分可以重复即可。比如 L 中，可以让 x 为空，把第一个字符选为 y 部分。此时 y 部分长度为 1 ＞ 0 ，xy 部分长度为 1 ≤ P，它重复无数次得到的字符串依然还属于 L。三个条件都符合。

然而这并没有什么用处……泵引理的作用在于证明一个语言非正则，所以真正有趣的是，给定一个非正则语言，如何在该语言中找到一个恰当的字符串，让它无论如何都不能拆成恰当的 xyz 三部分。

泵引理的实际运用

在实际使用泵引理证明一个语言非正则的时候，要使用反证法：假设该语言正则，那么它理应满足泵引理，然后我们证明它满足不了泵引理，因此它是非正则的。也就是前边说的，关键在于如何找到一个恰当的字符串，让它无论如何都不能拆成恰当的 xyz 三部分。

Shai Simonson 在 ADU 的课上介绍了一种角色扮演的方法非常有用：

语言 L’= {0m1n / n = m} 是一个非正则语言。因此并没有一个有穷机与其对应。一个人声称自己设计出了接受 L’ 的有穷机 M’，因此 L’ 是正则的。我们就可以与对手进行以下辩论，最终击败他。

Round 1 有穷机 M’ ：

对手声称构建出了 M’，它可以接受 L’。我们的观点是他不可能构建出这个有穷机，所以他的 M’ 一定是错误的。

我们先询问对手他的 M’ 有多少个状态，假设他的答案为 N 个状态（N可以为任意正整数）。

然后我们取 L’ 中的字符串 s’ = 0N1N。既然这个字符串属于 L’，那么对手的机器 M’ 一定可以接受它。

既然如此，就让对手试着输入 s’ 到他的机器 M’ 。由于s’ 长度为 2N，所以当它输入到 M’ 中时，一定在运行中出现了循环。进一步说，由于机器 M’ 一共只有 N 个状态，所以在运行时，循环应该在接收前 N 个字符输入期间就出现了。（鸽笼原理）

让对手告诉我们循环到底出现在什么位置，假设他说出现在第 i 个字符到 第 j 个字符之间。

根据前边的推论，既然 s’ 的前 N 个字符都是 0， 而 i、j 又一定小于等于 N，那么 i 到 j 之间所有字符都应该是 0。这种情况下，我们在 i、j 之间多循环几遍应该对结果毫无影响，也就是重复第 i 到第 j 个 0，得到的新字符串应该还在 L’ 中。

但事实上这肯定是不成立的，一旦重复，0 的数量就会超过 1 的数量，也就是说这个新的字符串不再属于 L’。出现了矛盾。

因此对手的机器 M’ 一定是错误的。

注意，在上面过程中对手有权给机器 M’ 指定任意长度及循环出现的位置。

Round 2 语言 L’：

这次抛开机器直接从语言角度辩论。对手声称 L’ 是正则的，它可以满足泵引理。我们的任务是找出字符串 s ∈ L’，并证明它无法划分成 xyz 并满足泵引理中的三个条件。

我们首先让对手给出 L’ 的泵长度，假设对手称其为 P。那么我们就可以拿 s = 0P1P开刀: s 长度为 2P ，大于 P，所以理应可以划分成 xyz 并满足三个条件。

既然 s 的前 P 个字符都是 0，根据条件中的 /xy/ ≤ P，我们知道不管对手怎么划分 xyz， xy 部分肯定都是 0。

接下来我们让对手任意选择 y 的部分，既然 xy 都是 0， y 必定也都是 0。

然后我们把 y 部分重复，得到新的字符串，这个字符串中 0 的数量必定超过 1，所以它不属于 L’。

也就是说， s 并没有满足泵引理第一个条件。更正式的记法为 0P-i0i0i1P ∉ L’。

因此 L’ 不是正则的。

注意，在上面的过程中对手有权指定任意泵长度及按照任意方法划分 xyz 部分。证明人则有权在一开始选择字符串，及对对手给出的 y 做任何处理，也就是制定重复次数 i 的值（重复 0 到无限多次皆可，只要能引发矛盾就行）。

最后

  1. 具体如何选择正确的字符串，以及如何对 y 做正确处理从而产生矛盾，并没有明确的算法，需要靠一点思考。
  2. 泵引例只能用来证明一个语言是非正则的，但不能说一个语言符合泵引理所以就是正则的。实际上有的非正则语言，依然满足泵引理。比如 L’= {0m1n / n、m 都是复数}。
  3. 更复杂上下文无关语言也有自己的泵引理，这里不做讨论。